Present Value of an Annuity
1. Definition and Formula
The formula below calculates the current value of a stream of equal payments (pmt) made at regular intervals over a specified period of time (n) at a given rate of interest (i). Such an arrangement is referred to as an annuity and the current cumulative value of all the payments is referred to as the present value (PV) of an annuity.
The present value of an annuity can be calculated as:

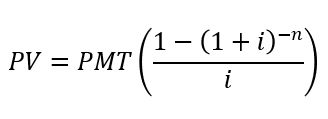
where:
PV = present value
PMT = periodic payment
i = interest rate
n = number of compounding periods
2. Example
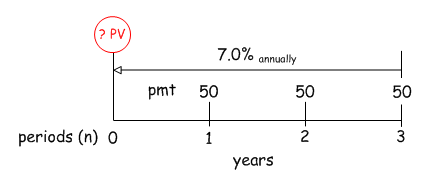
You agree to sell an asset for a series of three annual payments of $50 starting one year from today. What is the current value of the offer if the prevailing rate of interest is 7% compounded annually?
The problem statement provides values for three of four variables needed to solve for the present value of the annuity: three equal annual payments $50 (PMT) will be received over a three-year period (n) starting next year. These payments are “discounted” at 7% (i) to value the offer in today’s dollars (PV).
Thus, three annual payments of $50 to be received starting next year are worth $131.22 in today’s dollars at 7% annual interest.
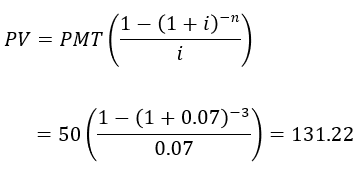
3. Concept
The mechanics of the discounting are illustrated here. Working backwards from $100 at 5% we see that this amount is worth only $95.24 if it were to be received in 1 year; $90.07 in 2 years; and $86,38 in 3 years.
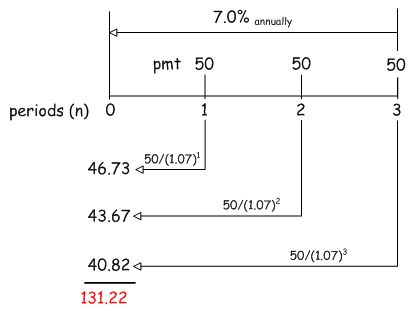
In essence what “present value” means is that the receipt of $100 in three years’ time is worth the same as $86.38 today. The logic behind this assertion is that if we deposited $86.38 into an investment account paying 5% annually, it would grow to $100 in three years. In this case we should be indifferent as to our preference for receiving the money today or in three years because the two amounts can be considered financially equivalent.
Of course this is not entirely true. In reality there are a host of other factors to consider before we can declare “equivalence.” However, some of these factors (i.e., taxes, inflation, liquidity, credit risk, etc.) can be accounted for by choosing an appropriate interest (discount) rate.
While not precise, time value theory can still serve as a powerful tool for analyzing financial alternatives by providing a mechanism for placing cash flows at different time periods on a comparable basis.
